Problem H
Godishalsbandet
Alice vill dela ett godishalsband med Bob. Halsbandet består av vita och blåa godisar. För att vara rättvis vill Alice dela halsbandet i två delar med lika många godisbitar i varje. Dock gillar Alice de blåa godisarna mycket mer än de vita, och vill därför få så många blåa godisar i sin halva som möjligt.
Vad är det största antalet blåa godisar Alice kan få i sin del, om hon klipper halsbandet optimalt?
Indata
Indatan består av en rad med en sträng som beskriver halsbandet. Strängen består endast av bokstäverna B och V, och har totalt ett jämnt antal bokstäver.
Utdata
Skriv ut en rad med ett heltal: det maximala antalet blåa godisar Alice kan få i sin del av halsbandet.
Poängsättning
Din lösning kommer att testas på en mängd testfallsgrupper. För att få poäng för en grupp så måste du klara alla testfall i gruppen.
|
Grupp |
Poängvärde |
Gränser |
|
$1$ |
$20$ |
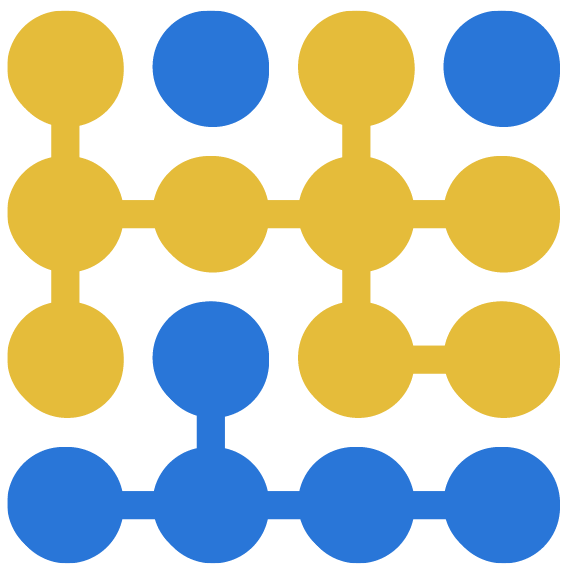
Halsbandet ser ut så som i figur 1. |
|
$2$ |
$40$ |
Halsbandet består av högst $1\, 000$ godisar. |
|
$3$ |
$40$ |
Halsbandet består av högst $10^6$ godisar. |
![\includegraphics[width=0.5\textwidth ]{group1}](/problems/godishalsbandet/file/statement/sv/img-0001.png)
Förklaring av exempelfall 1
BBVVBVVVBB har längd 10 så Alice måste dela halsbandet i två delar med $5$ godisar i varje. De möjliga delarna hon kan få är BBVVB, BVVBV, VVBVV, VBVVV, BVVVB, VVVBB, VVBBB, VBBBB, BBBBV, BBBVV. Hon får mest blåa godisar genom att välja VBBBB eller BBBBV som har $4$ blåa godisar.
![\includegraphics[width=0.5\textwidth ]{sample1}](/problems/godishalsbandet/file/statement/sv/img-0002.png)
| Sample Input 1 | Sample Output 1 |
|---|---|
BBVVBVVVBB |
4 |
| Sample Input 2 | Sample Output 2 |
|---|---|
BVBVBVBV |
2 |
| Sample Input 3 | Sample Output 3 |
|---|---|
BBVBVVVBBVVBBBVBVVBV |
6 |